Image Stack Computation

Compute and modify channels in an image using expressions. There are two main ways to use this. One is to use the toolbar to create an image stack using expressions. You can compute multiple channels. For this you specify a grid using xmin,xmax,ymin,ymax,zmin,zmax and the grid size. The expression can depend on the coordinate (x,y,z) of each grid point.

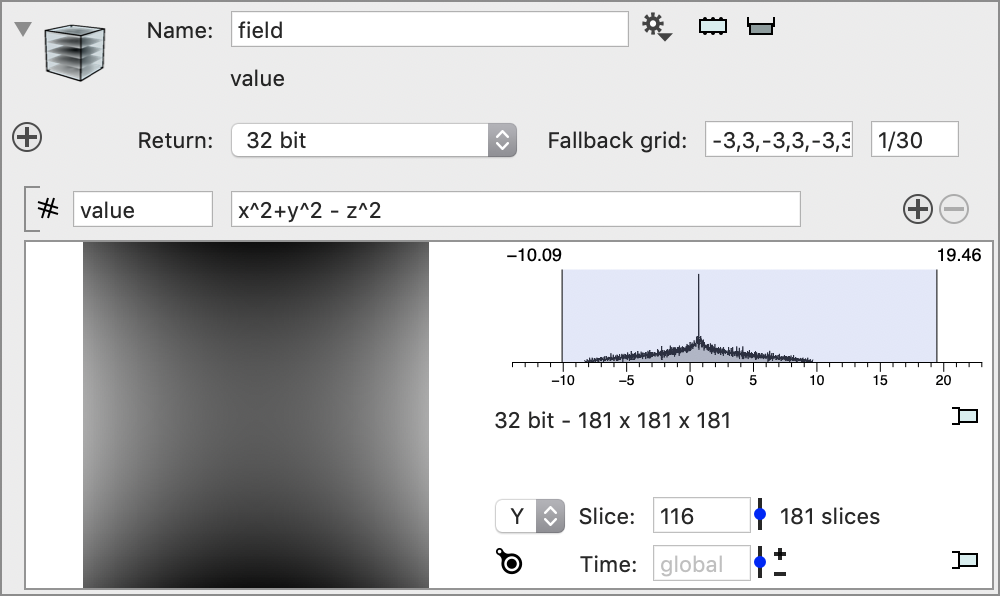
You can also use different grid sizes in x,y,z

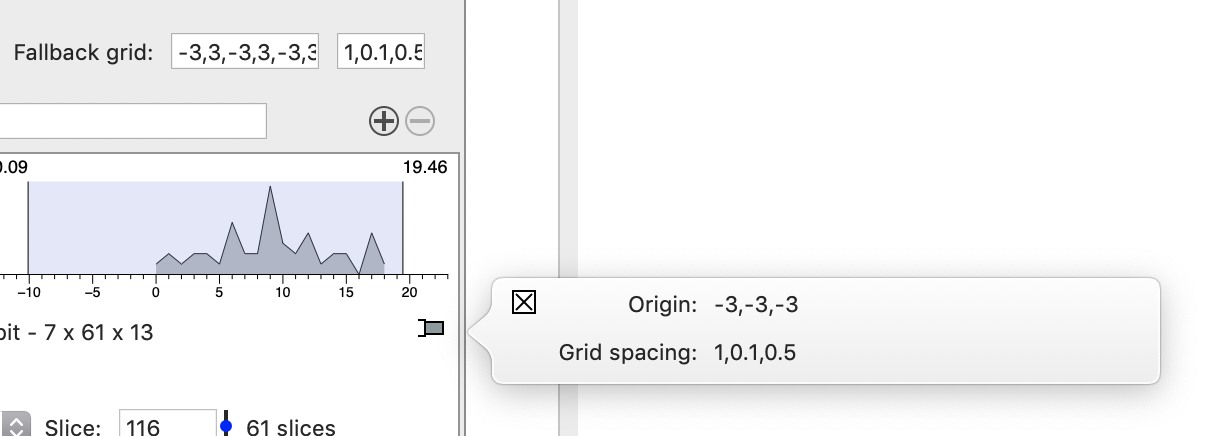
This means that your voxels are not cubes.

Another way to get to this same action is by using the Image Computation action in the gear menu for a Image Stack variable. This is the same as before but you already have a local variable defined and connected to the image stack you started with.

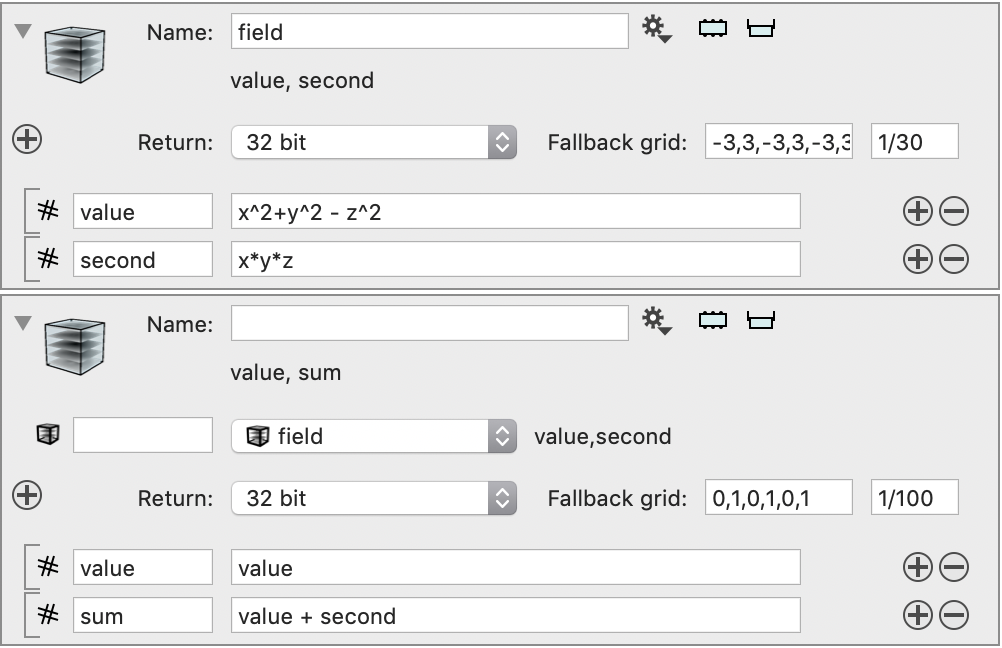
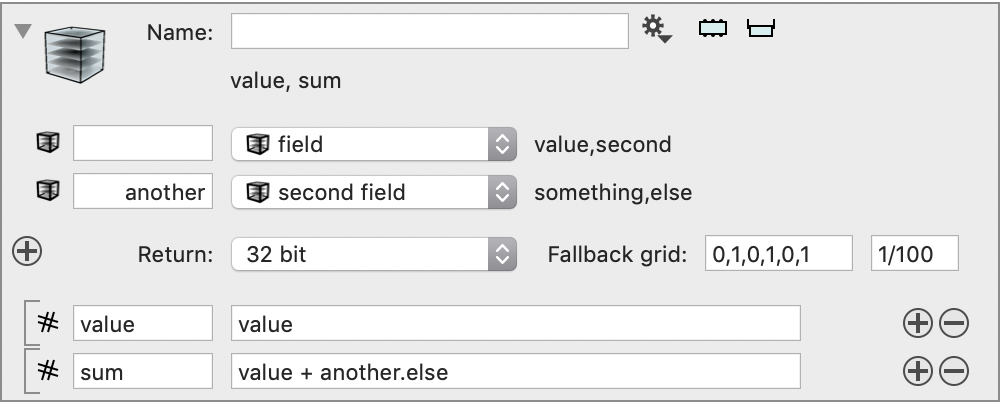
Because the image stack has values defined you don’t need a name for the local variable and you can refer to the channel names directly. You can add additional image stacks, but these have to all have the same grid.

The fallback grid is not used in this case because the grid can be deduced from the input variables. If you don’t specify a name here the channel names get added to the list of variables that can be used. If a name is repeated you can give this entry a name and then use a “.” notation to access a specific channel in that image stack. This is for example useful if you want to subtract a background from an image.

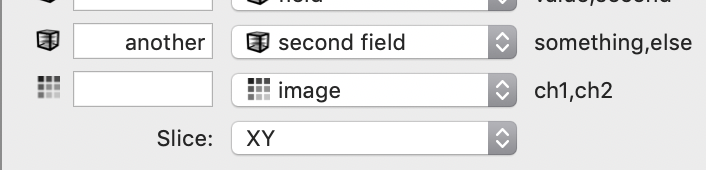
The local variable menu has the standard entries but in addition to the image stack you can also select a two dimensional image and a 3D mask. The 3D mask entry needs to have a name since there are no channels for that variable. The 2D image option asks you to specify a plane for the image. The image is then replicated in each coordinate plane.

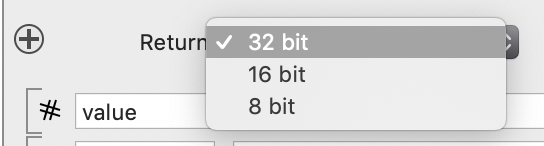
The image is by default 32 bit, a floating point number. You can specify 16 and 8 bit which are integer representation (non-negative). The expression itself is computed using floating point calculations but then rounded to the nearest integer and restricted to the range [0,255] for 8 bit and [0,2^32-1] for 16 bit.

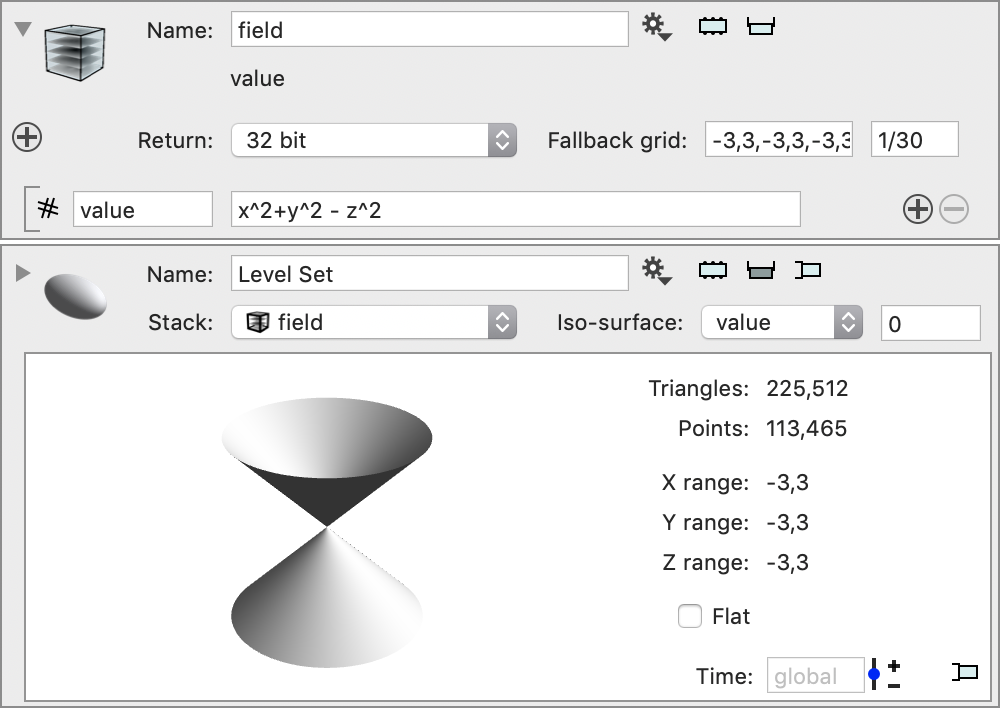
Example

To visualize the surface

x^2 + y^2 = z^2

we note that this is equivalent to

x^2 + y^2 – z^2 = 0

So compute the expression on the left side on a grid around the origin, and then use the gear menu to compute a thresholded surface at 0.