Signed Distance
The signed distance computes the distance from a polygon on a uniform grid.
The following screenshot shows a path created by a parameterized function for the x and y coordinates. It starts at (1+scale,0) and traverses counterclockwise until it ends at the same point that it started. This gives you a closed path.
To create the distance, use the Gear menu and select the “Signed Distance” option. You can choose an existing image variable to specify the grid, but here, we specify it using the region [-2,2] in the x direction and [-1.5,1] in the y direction. This gives you a 401 by 301 grid.
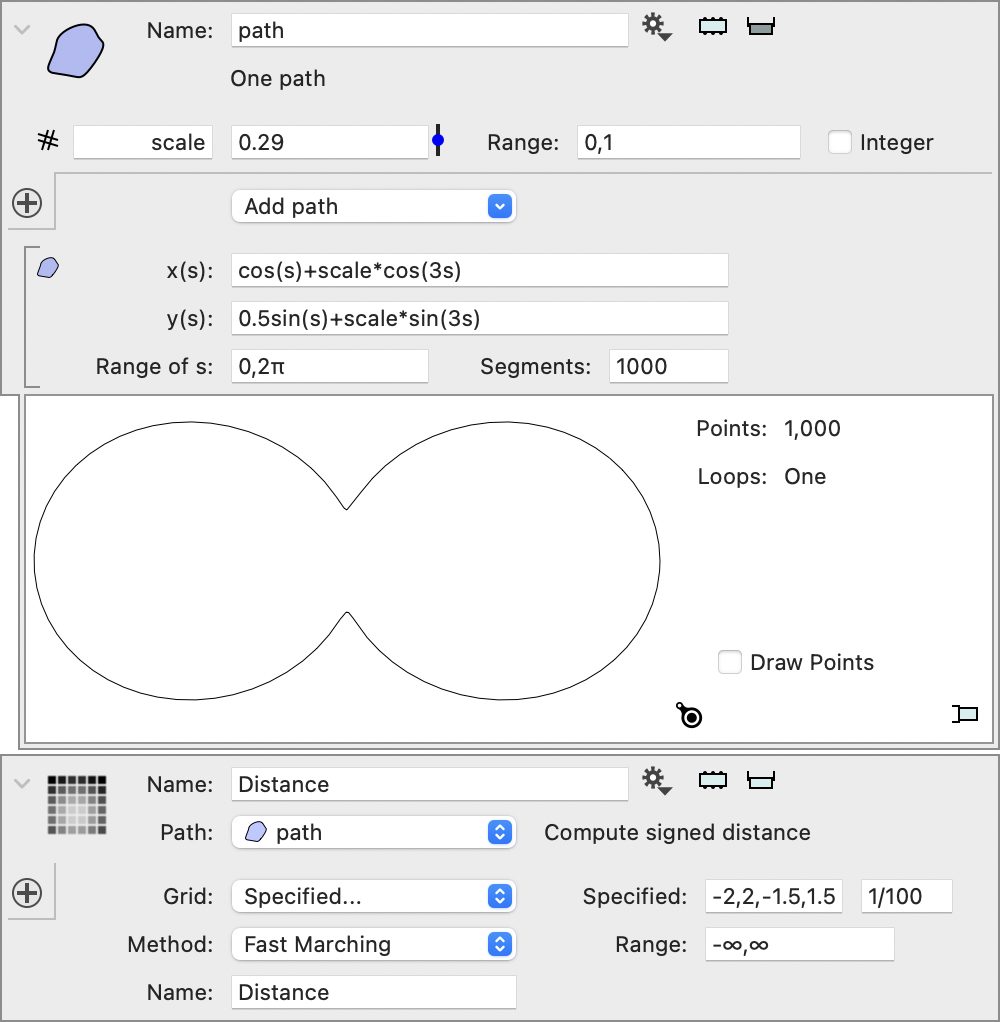
For each point in the domain, the distance is defined as the distance to the closest point on the path.
There are two methods to compute the signed distance. Most of the time, you use the Fast Marching method, which is https://en.wikipedia.org/wiki/Fast_marching_method. The Full distance computes the exact distance to the polygon.
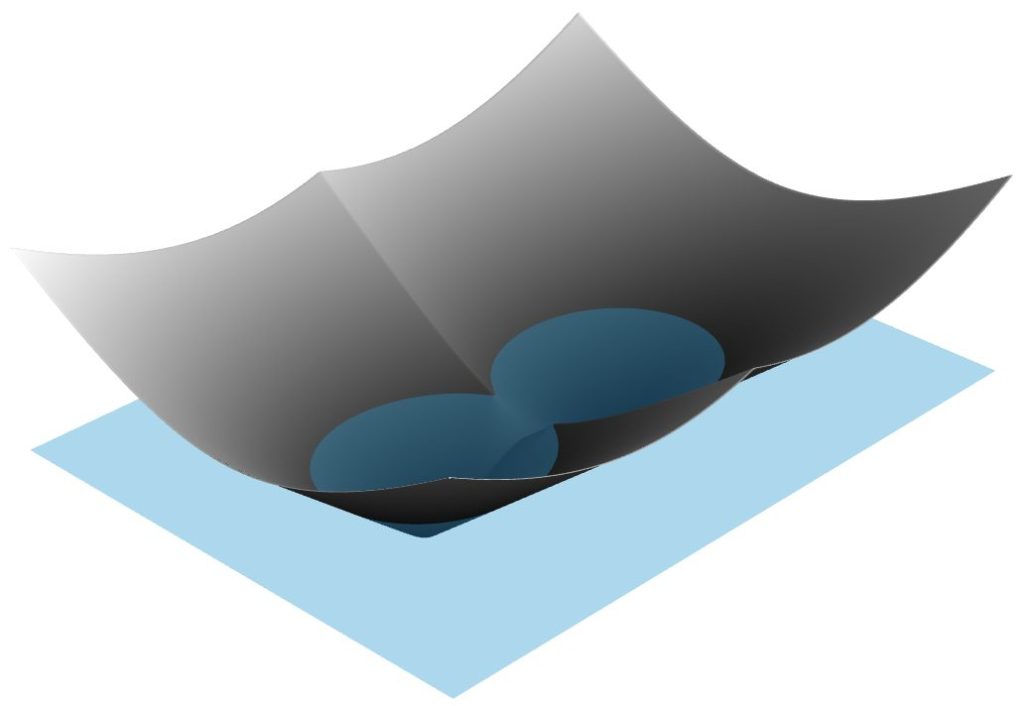
If you draw the distance in the z-direction, you get a result where the zero value (slicing plane) replicates the path (how well it replicates depends on the step size). The sign is picked to be positive on one side and negative on the other. The sign depends on whether the path is oriented in a clockwise direction (as this path is) or counterclockwise. For a counterclockwise path, the sign is flipped. One way to view that is that if you travel along the path on your right, the value will be positive, and on your left, it will be negative.
To understand the execution speed, say you have an N x N grid and want the distance everywhere. Further, assume that the number of line segments in the polygon is S. For the full distance, the cost is O(N^2 s). The cost is O(N^2 log(N)) for the fast marching distance. For high accuracy, s is typically large enough that the fast marching is much faster. Technically, the cost is O(N^2 log(N))+O(s+N), but the second part is dwarfed by the first part for all reasonable s values.
However, if you only want a band of k pixels around the computed, the cost of the full method changes to O(k^2 s) for reasonable s, and the fast marching is O(Nk log(N)). In this case the speed difference is minimal and the improved accuracy might be worth it.
You can specify the band by setting the Range parameter. Note that the range has to include the 0 point. For fast marching, you can use an asymmetric interval, but the full distance always gives you a symmetric interval.
Example uses
The distance map is used in several fields, including image processing and solving differential equations. One example is the Level Set method (https://www.sciencedirect.com/science/article/pii/S0021999185710984), which relies on the signed distance function.
One example is to offset a polygon. Compute the signed distance first. If you want to offset it by a distance D, take the level set/thresholded path with value D. The following screenshot shows the level sets at multiples of 0.1. One of the (when the threshold is 0) is the original path, the others are what happens when you dilate or erode the path.
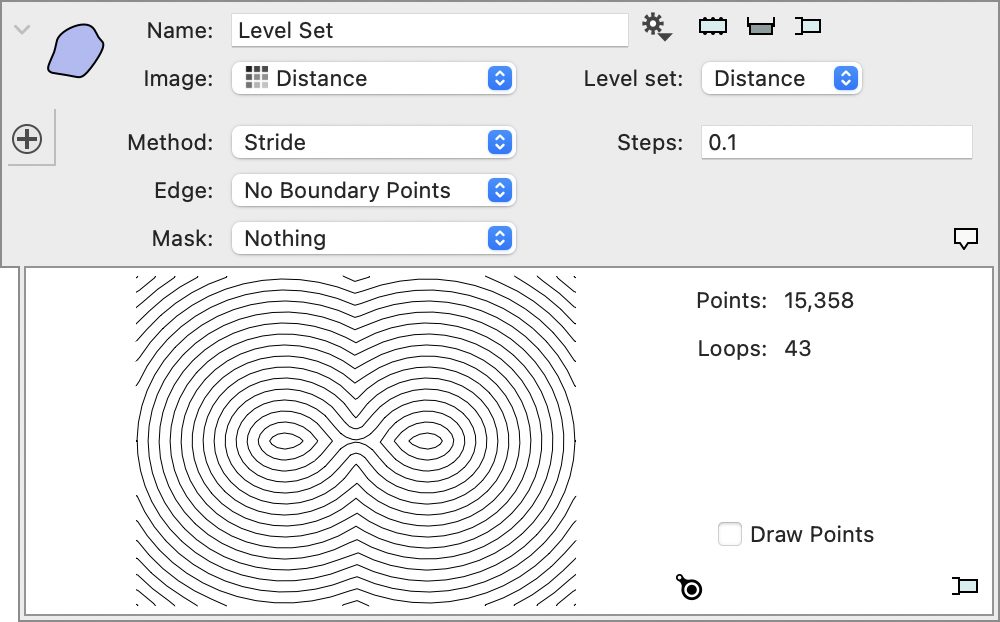
Another example is to use this as a pre-processing step for a watershed method. If you compute the signed distance and then find the local maxima/minima of the distance function, you can pick the centers of a dividing cell. The parametrized curve above roughly resembles a cell going through mitosis.