Shift Time

Variables can depend on time. The time could be physical time, but also used to label sequences and collections. Computations are done for the same time for all variables. There is an action to pick particular time values, and this action allows you to go to previous or subsequent time steps. There is a menu option for the immediatly previous time and the next time, but you can also go a fixed number of steps in each direction. Use the sign in the parenthesis as a guide to what sign to use.

Here is a simple example using the Group variable. The first entry creates a time sequence by adding a time series entry to the local variables. You can add this through the + button menu. This local variable is used to define the values t,v in the group. The goal is to compute a simple finite difference approximation for the first and second derivative in time. That needs you to reference the neighboring time values. For the screen shot below, the time slider was moved to t=2.

Use the gear menu to create this entry

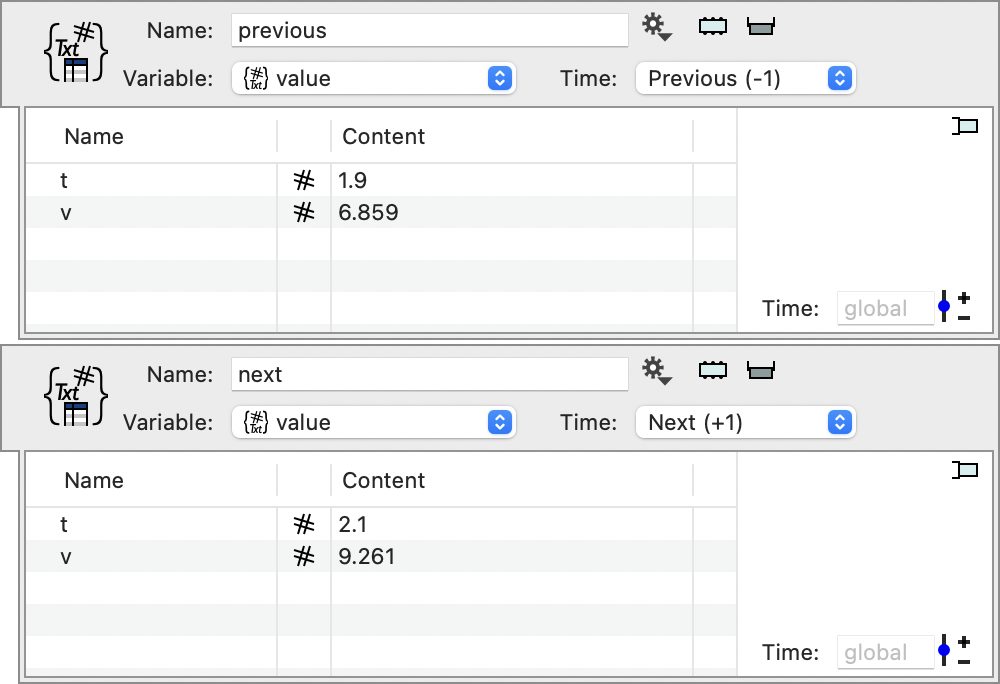
As you can see in the variable monitor, when the slider is at 2 the values for the previous and next come from the previous values.

If you show the cache for the top entry you see that there are three entries that have been computed.

Now you can use the new objects to pull in other time values into the computation. Create a new group variable and drag the three variables onto the + button for the local variables to add those references. You need to specify prefixes for two of them, otherwise the t and v value in the second and third entry will overwrite the previous definitions of t and v.

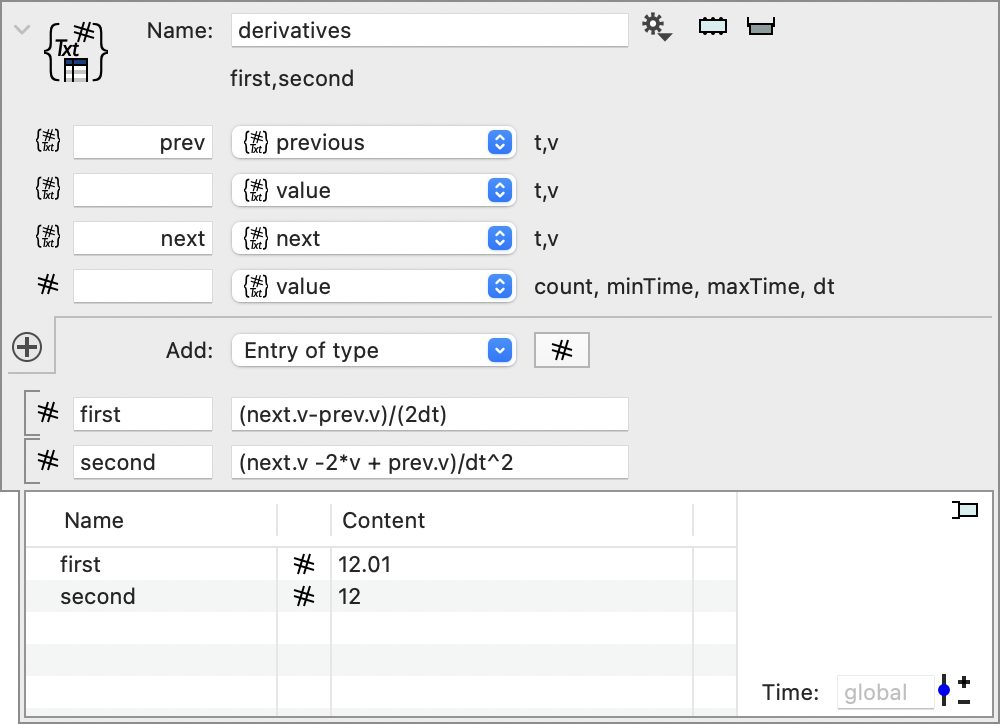
The last entry in the local variable is different from the previous three. That is the ‘Add Time Sequence Information’ entry. Select the ‘value’ variable. This adds the time step information into the local variables. The first and second are approximations to the first and second derivative of the value. The function is f(t) = t^3 that has first and second derivatives 3t^2 and 6t. At t=2 these derivatives are 12 and 12. These are approximations. There is clearly an approximation error for the first derivative, but the second derivative happens to be exact because the polynomial is low enough order.